2.Drawing

This chapter explains the concept of polygons, which is the basic concept of 3D graphics, and how to set polygons in SGL.

2-1. Polygon

A polygon consists of three or more vertices "v1, v2, v3, v4...vn" on the same plane. The closed area obtained by connecting these vertices in order such as v1 to v2, v2 to v3, v3 to v4, and finally vn and v1 is called a "polygon". Generally, the straight line connecting each vertex is called an "edge."

Figure 2-1 General polygon example

A polygon is valid if the number of vertices is 3 or more, but it is generally said that a polygon with 3 or 4 vertices is optimal (SGL only supports polygons with 4 vertices).

2-2. Polygons in SGL

SGL only supports polygons with 4 vertices. For this reason, polygons with 3 or 5 or more vertices cannot be expressed. However, by setting two of the four vertices to the same coordinates, you can draw a polygon with three vertices in appearance.
Edges are always joined clockwise, regardless of vertex number.

Figure 2-2 Polygon example on Sega Saturn

On the Sega Saturn, polygons are drawn as filled areas on the screen. The steps to draw polygons are as follows.

1. Creating a vertex coordinate list
2. Creating a polygon face list
3. Determine surface attributes for each polygon face
4. draw on screen

Next, we will explain the related functions and function parameters with reference to an actual drawing routine.

Polygon drawing routine

When actually drawing polygons in SGL, use the library function “slPutPolygon”. This function draws the polygon specified as a parameter, but the display position and various conversion operations (rotation, translation, scaling) follow the current matrix.

[void slPutPolygon ( PDATA *pat );]

Draws data-defined polygons.
Assign to the parameter the start address of the area where the polygon data table containing the polygon vertex data list, number of vertices, face list, number of faces, and face attribute data is stored. For details on parameters, please refer to the next section "Parameters required for polygon drawing".

Below, we will explain using a sample program.

In the sample program, after making the necessary preparations for drawing polygons (initialization, setting coordinates and display angles, etc.), the concept of a hierarchical matrix (see " Chapter 5: Matrix " for details) is used to display polygons. The position, display angle, scaling ratio (not used this time), etc. are determined, and the actual polygon drawing is performed based on these data.
The library function “ slPutPolygon(&PD_DATA): ” is used to draw polygons.
“&PD_DATA” in parentheses is a variable that collectively contains the parameters necessary for displaying polygons, and is defined in the data file “ polygon.c ”.
(See “Listing 2-2: polygon.c: Polygon parameters”).

Listing 2-1 sample_2_2: Polygon drawing routine

/*------------------------------------------------ ----------------------*/
/* Draw 1 Polygon */
/*------------------------------------------------ ----------------------*/
#include "sgl.h"

extern PDATA PD_PLANE1;

void ss_main(void)
{
	static ANGLE ang[XYZ];
	static FIXED pos[XYZ];

	slInitSystem(TV_320x224, NULL, 1);

	ang[X] = ang[Y] = ang[Z] = DEGtoANG(0.0);
	pos[X] = toFIXED( 0.0);
	pos[Y] = toFIXED( 0.0);
	pos[Z] = toFIXED(220.0);

	slPrint("Sample program 2.2", slLocate(9,2));

	while(-1){
		slPushMatrix();
		{
			slTranslate(pos[X], pos[Y], pos[Z]);
			slRotX(ang[X]);
			slRotY(ang[Y]);
			slRotZ(ang[Z]);
			slPutPolygon(&PD_PLANE1);
		}
		slPopMatrix();

		slSynch();
	}
}

Flow 2-1 sample_2_2: Polygon drawing flowchart

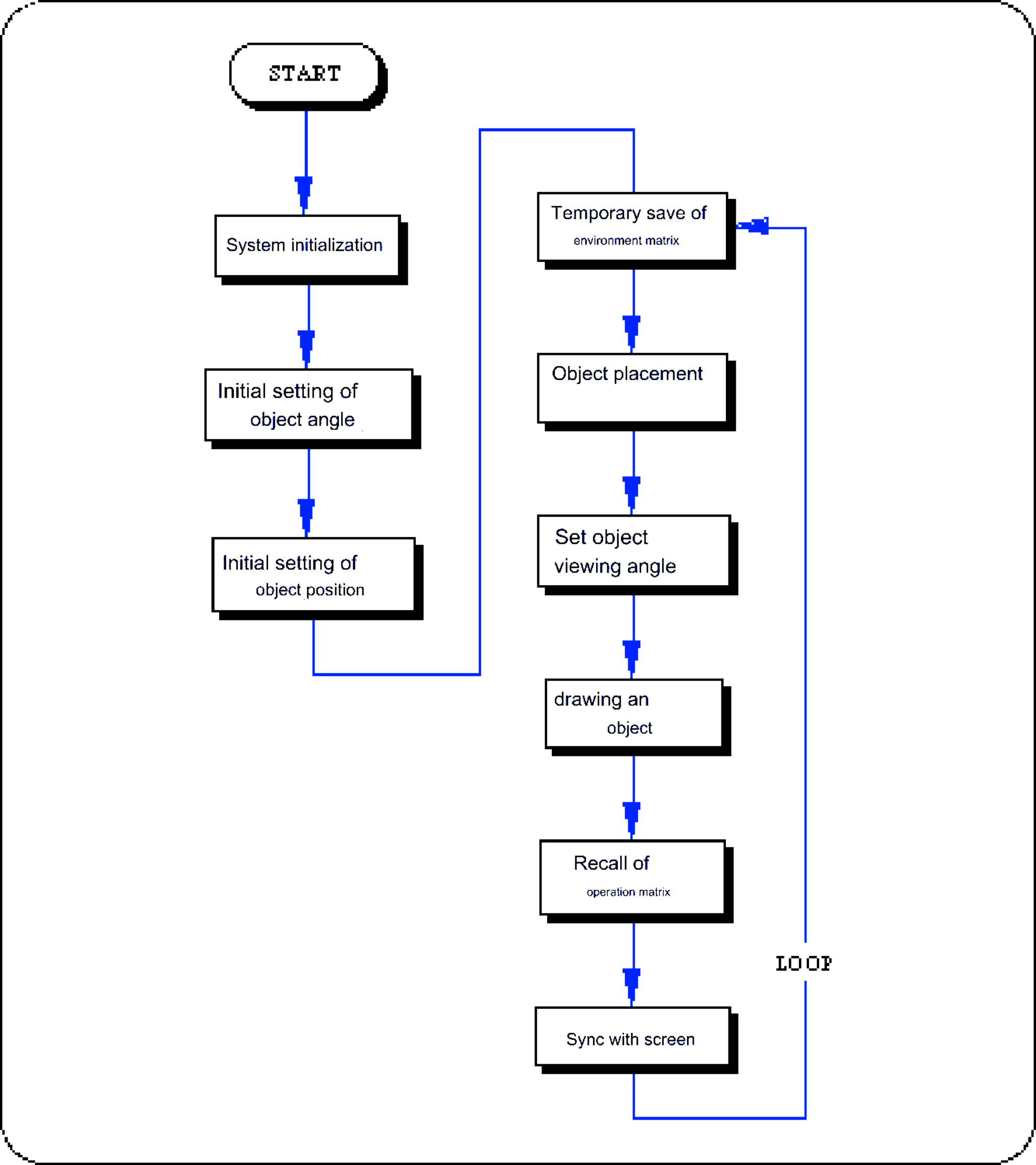
Parameters required for drawing polygons

The following list is the polygon drawing parameters that are loaded as “polygon.c” in the program. By rewriting this part, you can change the shape, size, number of faces, surface attributes, etc. of the polygon.

Listing 2-2 polygon.c: Polygon parameters＞

#include "sgl.h"

POINT point_PLANE1[] = {
        POStoFIXED(-10.0, -10.0, 0.0),
        POStoFIXED( 10.0, -10.0, 0.0),
        POStoFIXED( 10.0, 10.0, 0.0),
        POStoFIXED(-10.0, 10.0, 0.0),
};

POLYGON polygon_PLANE1[] = {
        NORMAL(0.0, 1.0, 0.0), VERTICES(0, 1, 2, 3),
};

ATTR attribute_PLANE1[] = {
        ATTRIBUTE(Dual_Plane, SORT_CEN, No_Texture, C_RGB(31, 31, 31), No_Gouraud, MESHoff, sprPolygon, No_Option),
};

PDATA PD_PLANE1 = {
        point_PLANE1, sizeof(point_PLANE1) / sizeof(POINT),
        polygon_PLANE1, sizeof(polygon_PLANE1) / sizeof(POLYGON),
        attribute_PLANE1
};

Figure 2-3 Drawing model using “polygon.c”

Figure 2-4 Procedure for creating a parameter data column

	●Numbers for vertex identification are automatically assigned in the order of "0, 1, 2, 3, 4, ~ n" from the top according to the order of the vertex list.
	●For each polygon surface, select any four points from the vertex list by vertex number to create a list of polygon surfaces. Also, if you use a light source, etc., also set the normal vector for each surface.
	●According to the order of the surface list, determine the attributes of the polygon surfaces starting from the top. Attributes include not only polygon color but also surface treatment method.
	●Calculate the number of vertices from the vertex list and the number of faces from the face list and add them to the list. Pass this as a polygon parameter to the drawing function.

Next, we will explain the steps for creating polygon data based on the data columns to be created.

[Create vertex list: POINT point_＜ label name＞ [ ]]

List of initial coordinates of polygon vertices. Identification numbers are automatically assigned to the vertices from top to bottom according to the order of the list: 0, 1, 2, 3, 4 ~ n.

Variable name: POS2FIXED ( vertex_x , vertex_y , vertex_z ),
Represents each vertex coordinate. By using the macro "POStoFIXED", floating point values can be substituted for coordinate values (POS2FIXED is a macro supported by SGL).

[Create surface list: POLYGON polygon_＜ label name＞ [ ]]

Create a list of polygon faces and normal vectors based on the vertex list.

Variable name: NORMAL (vector_x, vector_y, vector_z),
Define the normal vector for each face. A normal vector is used to express the direction of a polygon surface, and is a unit vector that extends perpendicular to the polygon surface.
Each parameter is an XYZ value that represents the direction of the radial vector, and the normal vector must always be specified as a unit vector.

Variable name: VERTICES ( v1 , v2 , v3 , v4 ),
Create a list of which vertices in the vertex list will be used to form a polygon surface. The number of vertices selected is always 4. However, only if the third and fourth vertex numbers are the same, a polygon that looks triangular can be expressed.
Also, there is no relationship between the vertex number and the order in which edges are joined. Edges are always connected clockwise starting from the first vertex selected by the list.

[Create surface attribute list: ATTR attribute_＜ label name＞ [ ]]

Set the polygon surface attributes for each face in the order of the face list.
For details on the settings, please refer to “Chapter 7: Polygon Surface Attributes”.

Variable name: ATTRIBUTE (plane, sort, texture, color, gouraud, mode, dir, option),

Sets surface attributes of polygons. Each parameter sets a total of 8 items: front/back detection, Z sort, texture, color, Gouraud processing, drawing mode, sprite reversal processing, and other functions.
(For details, refer to “Chapter 7: Polygon Surface Attributes”)

[Creating data string for drawing function: PDATA PD_＜ label name＞ ]

Create a data structure to pass each polygon data setting as a parameter to the library function “slPutPolygon”.

Variable name: Vertex list, number of vertices, surface list, number of surfaces, surface attribute list

Create the data column that will actually be passed to “slPutPolygon”.
Here, the number of vertices and the number of polygon faces are newly calculated from information such as the vertex list and added to the parameter data string.

Figure 2-5 “PDATA PD_＜ label name＞ ” parameters

●Polygon data structure●

PDATA PD_PLANE1={
	point_PLANE1, /* Vertex list */
	sizeof(point_PLANE1)/sizeof(POINT), /* Number of vertices */
	polygon_PLANE1, /* Plane list */
	sizeof(polygon_PLANE1)/sizeof(POLYGON), /* Number of planes */
	attribute_PLANE1 /* attribute list */
};

2-3. Combination of multiple polygons

When actually expressing some shape using polygons, it is impossible to achieve it with only one polygon. Therefore, here we will explain how to create data for an object using multiple polygon faces.

Creating a cube

To represent a cube, you need to set an object with 8 vertices and 6 polygon faces as parameter values.
In SGL, this can be achieved by rewriting the contents of the parameter setting data file "polygon.c" described above as follows.
In the list, first create a list of the eight vertices that form the basis of the cube, then create a list of six faces from these vertices, determine the surface attributes for each face, and then add each data to the parameter data string "PD_PLANE". Store it in By passing this as a polygon parameter to the drawing function “ slPutPolygon ”, the cube will be drawn on the screen.

Listing 2-3 below is an example of creating cubic polygon data.

Listing 2-3 polygon.c: Cube polygon parameters

#include "sgl.h"

POINT point_PLANE1[] = { /* Create vertex list */
	POStoFIXED(-15.0, -15.0, -15.0), /* Vertex coordinates (XYZ array) */
	POStoFIXED(-15.0, -15.0, 15.0),
	POStoFIXED(-15.0, 15.0, -15.0),
	POStoFIXED(-15.0, 15.0, 15.0),
	POStoFIXED( 15.0, -15.0, -15.0),
	POStoFIXED( 15.0, -15.0, 15.0),
	POStoFIXED( 15.0, 15.0, -15.0),
	POStoFIXED( 15.0, 15.0, 15.0),
};

POLYGON polygon_PLANE1[] = { /* Create plane list */
	NORMAL(-1.0, 0.0, 0.0), /* Normal vector settings */
	VERTICES(0, 1, 3, 2), /* Vertex number to be selected in one plane */
	NORMAL( 0.0, 0.0, 1.0), 
	VERTICES(1, 5, 7, 3),
	NORMAL( 1.0, 0.0, 0.0), 
	VERTICES(5, 4, 6, 7),
	NORMAL( 0.0, 0.0, -1.0), 
	VERTICES(4, 0, 2, 6),
	NORMAL( 0.0, -1.0, 0.0),
	VERTICES(4, 5, 1, 0),
	NORMAL( 0.0, 1.0, 0.0),
	VERTICES(2, 3, 7, 6),
};

ATTR attribute_PLANE1[] = { /* Create plane attribute list */
	ATTRIBUTE(Dual_Plane,SORT_CEN,No_Texture,C_RGB(31,31,00),No_Gouraud,MESHoff,sprPolygon,UseLight),
	ATTRIBUTE(Dual_Plane,SORT_CEN,No_Texture,C_RGB(31,00,00),No_Gouraud,MESHoff,sprPolygon,UseLight),
	ATTRIBUTE(Dual_Plane,SORT_CEN,No_Texture,C_RGB(00,31,00),No_Gouraud,MESHoff,sprPolygon,UseLight),
	ATTRIBUTE(Dual_Plane,SORT_CEN,No_Texture,C_RGB(00,00,31),No_Gouraud,MESHoff,sprPolygon,UseLight),
	ATTRIBUTE(Dual_Plane,SORT_CEN,No_Texture,C_RGB(31,00,31),No_Gouraud,MESHoff,sprPolygon,UseLight),
	ATTRIBUTE(Dual_Plane,SORT_CEN,No_Texture,C_RGB(00,31,31),No_Gouraud,MESHoff,sprPolygon,UseLight),
};

PDATA PD_PLANE1 = { /* Create data column for drawing function */
	point_PLANE1,
	sizeof(point_PLANE1)/sizeof(POINT), /* Calculate the number of vertices */
	polygon_PLANE1,
	sizeof(polygon_PLANE1)/sizeof(POLYGON), /* Calculate the number of polygon faces */
	attribute_PLANE1
};

Figure 2-6 Drawing model with parameters in List 2-3
Note) Since it is a left-handed coordinate system, the positive Z-axis direction is at the back of the screen.

2-4. Polygon distortion problem

When viewing polygons, you may experience distortion issues.
Distortion is often caused by calculation errors.
It may also be due to the fact that the polygon vertices are first specified in 3D and then projected onto the 2D screen after a transformation operation.
The only distortion that makes a true polygon (a polygon whose vertices are all on the same plane) unrecognizable is when the polygon becomes a single line when viewed from the edge direction (horizontal to the polygon surface). One example is putting it away.

Additional notes: SGL library functions that appeared in this chapter

In this chapter, we explained the functions in the table below.

Table 2-1 SGL library functions that appeared in this chapter

functional type	function name	parameters	function
void	slPutPolygon	PDATA*pat	Drawing polygons (setting parameters)