Return to previous page | Return to menu | Go to next page

This chapter describes the basic idea of 3D graphics and the subroutine that realizes it. In this chapter, we will use a mathematical method called coordinate transformation. I think that it is difficult to read because it uses a little different from usual methods such as determinant operations, but it is the basic part of 3D graphics, so please read and understand it many times.
Objects projected by 3D graphics are generally defined by the following four.
Coordinate system: Determines the position and orientation of objects and viewpoints. Projection transformation: Defines how the image is projected on the projection surface. Modeling transformation: Defines movement, rotation, and scaling within the coordinate system. Viewing transformation: Defines the viewpoint and its movement (see “Chapter 6: Camera” for details).
By combining these four, 3D graphics can be projected on a monitor. Therefore, in this chapter, we will explain the three without the viewing conversion in order, and then add more detailed explanations.
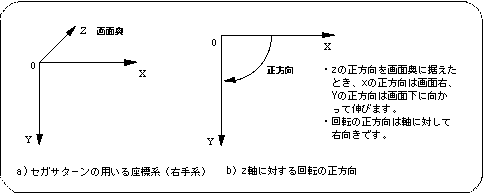
Sega Saturn uses a 3D coordinate system commonly called the right-handed coordinate system. This is a coordinate system where the positive direction of the Y-axis is the bottom of the screen and the positive direction of the X-axis is the right of the screen when the positive direction of the Z-axis is placed at the back of the screen. The direction of rotation is the right direction (clockwise) with respect to the axis.
Apart from this, SGL has a 2D coordinate system called screen coordinates corresponding to the TV monitor and screen mode (resolution). This is mainly used to handle 2D graphics such as scrolling and sprites, but it is also used when setting a window in “Section 4-5: Window”.
