Japanese
★ SGL User's Manual ★ PROGRAMMER'S TUTORIAL
▲ Back ｜ Forward ▼

8-9. Rotating scroll screen

The rotating scroll screen “RBG0” can be enlarged/reduced and rotated.
Also, although the idea is different from normal scrolling, it is also possible to move the scroll vertically and horizontally.
Here, we will explain the movement, scaling, and rotation functions of the rotating scroll along with a sample program.

Moving the rotating scroll

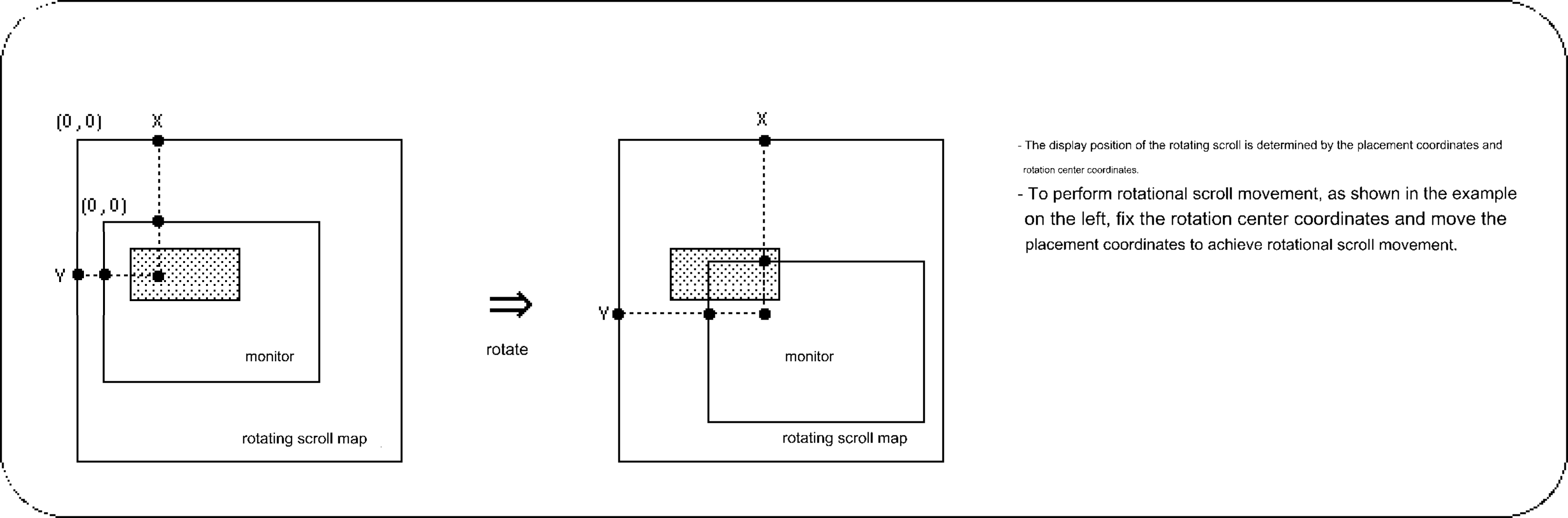
Rotational scroll movement is actually realized as a change in the scroll display position.
By using the function "slLookR", you can make it appear as if the scroll is moving vertically, horizontally, and vertically relative to the monitor.

Figure 8-21 Image of rotating scroll movement

Rotating scroll screen scaling

With SGL, it is also possible to scale the rotating scroll screen. Scaling of the rotating scroll screen is different from scaling of the normal scroll screen, and it is always possible to zoom in or out at any magnification.
In addition, in the case of a rotating scroll screen, it can also be used in combination with the scroll rotation operation, enlargement/reduction operation, and movement operation described later.
If you want to scale the rotating scroll screen using SGL, please use the library function "slZoomR".

[void slZoomR ( FIXED scale_x , FIXED scale_y ) ;]
Scales the rotation scroll screen "RBG0" and saves the current state to the current rotation parameter (the current parameter can be switched with the function "slCurRpara").
Assign the scroll vertical and horizontal magnification as reciprocal numbers to the parameters.
For example, if you want to enlarge it by 2 times, assign 1/2 to the parameter, and if you want to reduce it by 1/2, assign 2 to the parameter.
For rotary scrolling, scaling can always be set to any desired magnification.

Rotate scroll screen rotation

On the Sega Saturn, it is possible to rotate the rotating scroll screen using any axis and arbitrary angle value.
(The image below is an image model).

Figure 8-22 Scroll rotation image
●2D rotation (Z-axis rotation)
If you want to perform 2D rotation operation (Z-axis rotation) on the rotating scroll screen in SGL, please use the library function "slZrotR".
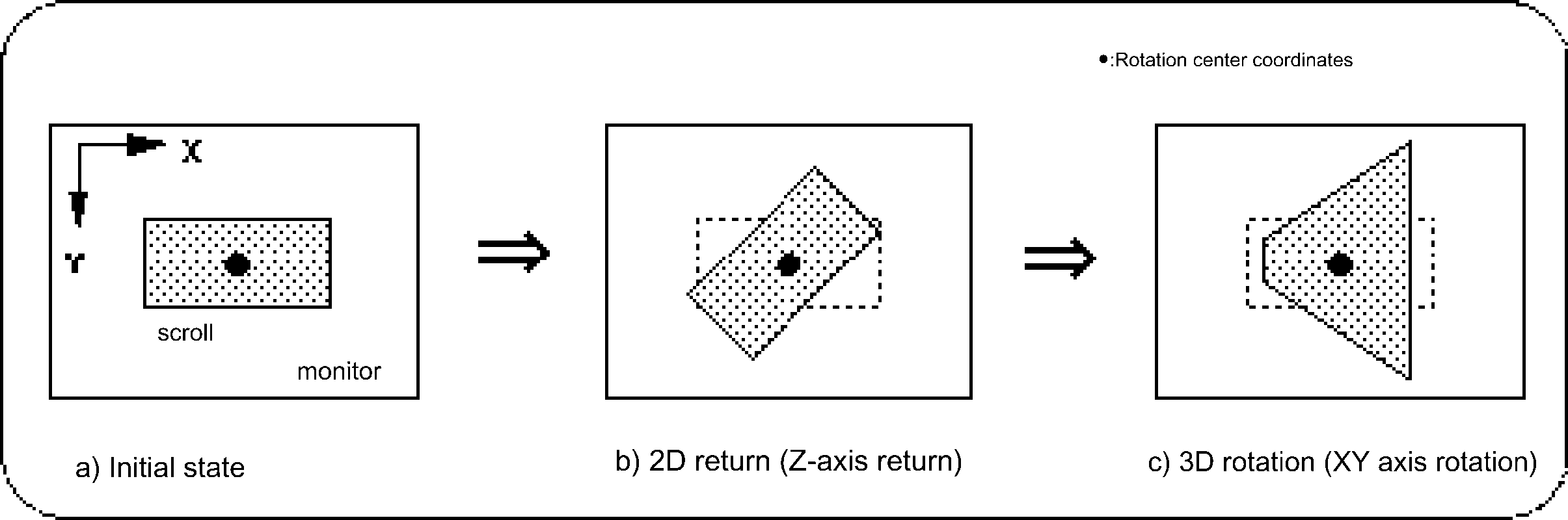
The point set by the library function "slDispCenterR" is used as the rotation center point (one point on the scroll map).

[void slZrotR (ANGLE z_angle);]
Rotate the rotating scroll screen “RBG0” about the Z axis.
Specify the Z-axis rotation angle of the current rotation parameter in the parameter.
For the rotation angle, substitute the absolute rotation angle value, not the rotation angle value from the current state.
(The current parameter can be switched using the function “slCurRpara”).
Also, the point set by the library function “slLookR” is used as the center of rotation.

Figure 8-23 Actual behavior of scroll rotation
Notes on function usage
The function group “slZrotR”, “slZoomR”, and “slLookR” used for rotational scroll conversion operations are the same rotation parameters as the function “slScrMatSet” that also performs various rotation scroll conversion operations (including 3D rotation). , please note that they cannot be used together.
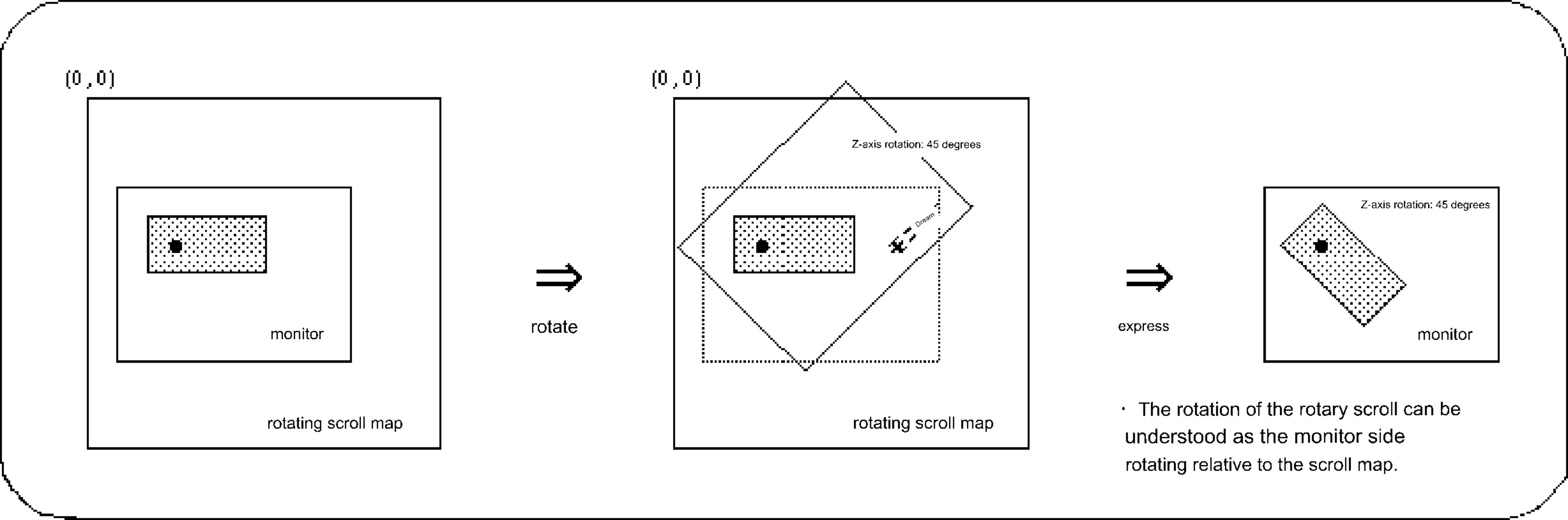
This is because the function group described above rewrites a specific area of the rotation parameter, whereas the function group described later rewrites the entire rotation parameter.

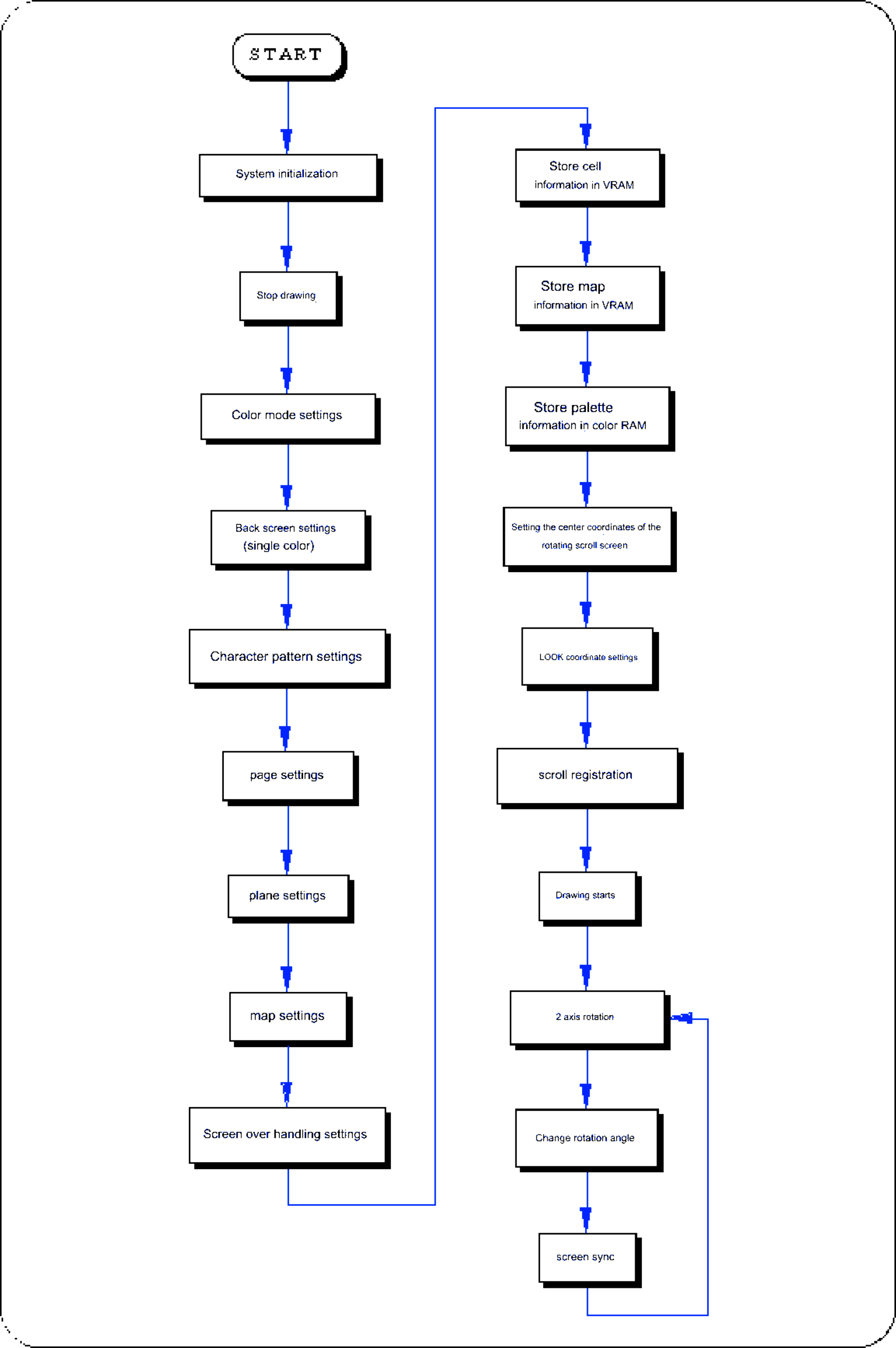
The following sample program (Listing 8-5) is an example of actually rotating a rotating scroll screen using SGL library functions.

Listing 8-5 sample_8_9_1: 2D rotation of scroll

/*------------------------------------------------ ----------------------*/
/* Graphic Rotation */
/*------------------------------------------------ ----------------------*/
#include "sgl.h"
#include "ss_scroll.h"

#define RBG0_CEL_ADR VDP2_VRAM_A0
#define RBG0_MAP_ADR VDP2_VRAM_B0
#define RBG0_COL_ADR ( VDP2_COLRAM + 0x00200 )
#define RBG0_PAR_ADR ( VDP2_VRAM_A1 + 0x1fe00 )
#define BACK_COL_ADR ( VDP2_VRAM_A1 + 0x1fffe )

void ss_main(void)
{
	ANGLE yama_angz = DEGtoANG(0.0);
	FIXED posx = toFIXED(128.0) , posy = toFIXED(64.0);
	
	slInitSystem(TV_320x224,NULL,1);
	slTVOff();
	slPrint("Sample program 8.9.1" , slLocate(9,2));

	slColRAMMode(CRM16_1024);
	slBack1ColSet((void *)BACK_COL_ADR , 0);

	slRparaInitSet((void *)RBG0_PAR_ADR);
	slCharRbg0(COL_TYPE_256 , CHAR_SIZE_1x1);
	slPageRbg0((void *)RBG0_CEL_ADR , 0 , PNB_1WORD|CN_10BIT);
	slPlaneRA(PL_SIZE_1x1);
	sl1MapRA((void *)RBG0_MAP_ADR);
	slOverRA(2);
	Cel2VRAM(yama_cel , (void *)RBG0_CEL_ADR , 31808);
	Map2VRAM(yama_map, (void *)RBG0_MAP_ADR, 32, 16, 1, 0);
	Pal2CRAM(yama_pal , (void *)RBG0_COL_ADR , 256);

	slDispCenterR(toFIXED(160.0) , toFIXED(112.0));
	slLookR(toFIXED(128.0) , toFIXED(64.0));

	slScrAutoDisp(NBG0ON | RBG0ON);
	slTVOn();

	while(1){
		slZrotR(yama_angz);
		yama_angz += DEGtoANG(1.0);
		slSynch();
	} 
}

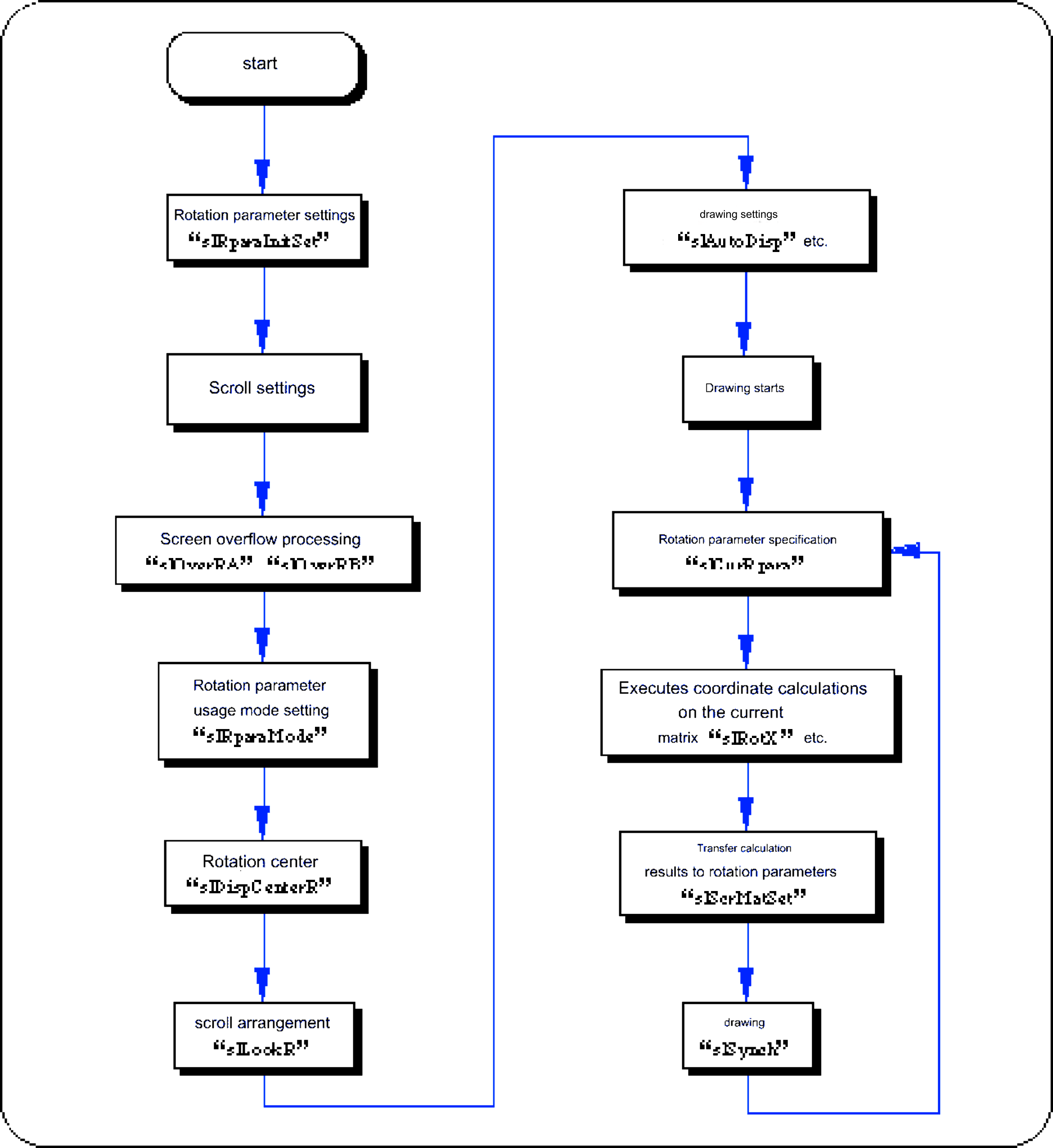
Flow 8-6 sample_8_9_1: 2D rotation of scroll

●3D rotation using current matrix
To perform 3D rotation operation (rotation on all axes) of a rotating scroll screen using the current matrix in SGL, you need to follow the steps below.

1) Rotating scroll settings
Complete various settings required for using rotary scrolling, such as rotation parameter settings, screen overflow processing, and coefficient table settings.

2) Coordinate calculation
First, perform the 3D rotation operation to multiply the rotation scroll on the current matrix.
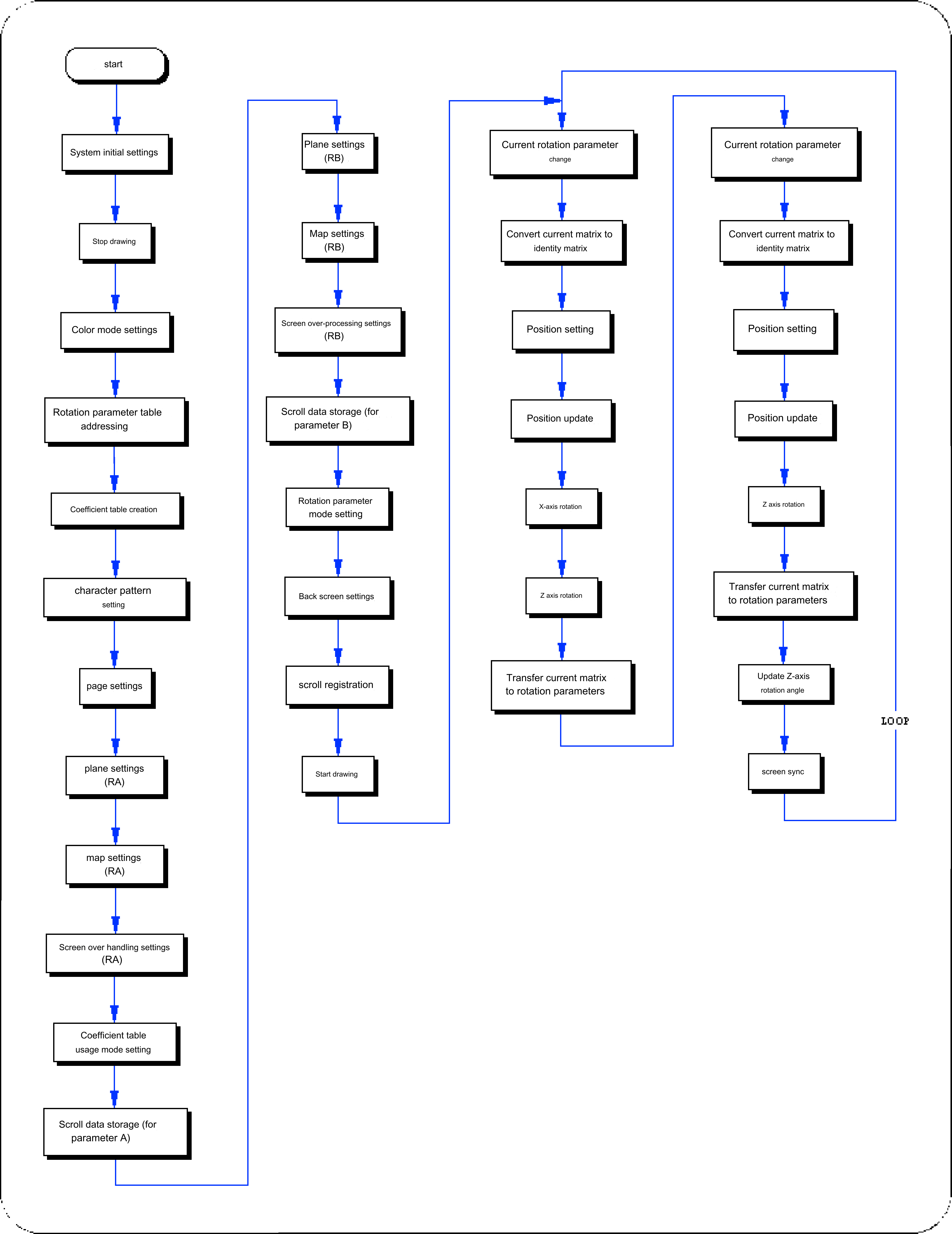
The same functions are used, such as “slRorX”, “slTranslate”, and “slScale”.
However, the order of rotation, movement, and scaling operations is the opposite of that of normal coordinate transformation operations (see "Chapter 4: Coordinate Transformation" for the order of transformation operations).
Also, the scroll coordinate system is a left-handed coordinate system because the positive and negative of the Z axis are reversed, but since the monitor rotates in response to scrolling, it looks exactly the same.
If you want to perform a coordinate conversion operation using the same matrix operation procedure as a normal coordinate conversion operation, please use the function “slScrMatConv” before transferring matrix data.
The function “slScrMatConv” converts the current matrix transformed using the normal coordinate transformation procedure into a coordinate transformation matrix for scrolling and makes it the current matrix.

[void slScrMatConv ( void );]
Converts the current matrix to coordinate transformation data for scrolling and replaces the current matrix.
Naturally, if you use this function on the current matrix after executing the scrolling coordinate transformation operation, the current matrix will be replaced with the normal coordinate transformation matrix.

3) Transfer calculation results to rotation parameters
Transfers the coordinate calculation results performed on the current matrix to rotation parameters.
Rotating scrolls are transformed and drawn based on the rotation parameter data that is transferred as a calculation result.
Use the function “slScrMatSet” to transfer data.

[void slScrMatSet ( void );]
Transfers the current matrix data to the current rotation parameter.
Please use it to transfer the current matrix that has been subjected to coordinate transformation operations according to rotational scrolling.

Flow 8-7 Procedure for 3D rotation operation using current matrix

●Controlling zoom ratio using coefficient table
When performing a 3D rotation operation on a rotating scroll, the rotating scroll scales the scroll according to the scroll depth. Normally, this scale ratio is calculated based on each parameter used in 3D coordinate calculations such as perspective transformation, and the scroll is transformed. However, this transformation ratio can be set in advance in units of lines or dots to transform the scroll. It can be used at runtime and is called a coefficient table.
When using the coefficient table, the following two functions are required.

1) Creation of coefficient table
First of all, you need to reserve an area for the coefficient table in the VRAM area.
Be sure to create the coefficient table in VRAM.
Also, the coefficient table occupies one bank in the VRAM area. This is because the coefficient table references the VRAM area for the maximum number of accesses per bank (8 times).

[void slMakeKtable ( void *adr );]
Creates a coefficient table to be used in 3D rotation operations at the specified address.
Assign the start address of the area where the coefficient table will be created to the parameter.
Also, the coefficient table must be allocated in the VRAM area.

2) Setting the coefficient table usage mode
When using the area specified as a coefficient table as a coefficient table, determine the usage mode of how the coefficient table is used.

[void slKtableRA,RB ( void *table_adr , Uint16 mode );]
Specify the address of the coefficient table to be used, and also determine the contents of the coefficient table.
Assign the starting address of the coefficient table and the values shown in the figure below that indicate the coefficient table usage mode (can be used in conjunction with the or operator "|") to the parameters.
The function "slKtableRA" sets the coefficient table used by rotation parameter A, and the function "slKtableRB" sets the coefficient table used by rotation parameter B.

Figure 8-24 Parameter substitution value (mode) for “slKtableRA,RB”
Table usage: [K_OFF | K_ON ]|
Coefficient data size: [K_2WORD | K_1WORD]|
Coefficient mode: [K_MODE0 | K_MODE1 | K_MODE2 | K_MODE3]|
Line color: [K_LINECOL]|
Deformation unit: [K_DOT | K_LINE ]|
Fixed coefficient: [K_FIX ]|

note)
If fixed coefficient is specified for the parameter, it is assumed that the coefficient table has been prepared in advance, and the coefficient table calculation will not be executed in real time.

reference
For details on the coefficient table, refer to “HARDWARE MANUAL vol.2: VDP2 User's Manual”.

List 8-6 sample_8_9_2: 3D rotation

#include "sgl.h"
#include "ss_scroll.h"

#define RBG0RB_CEL_ADR (VDP2_VRAM_A0 )
#define RBG0RB_MAP_ADR (VDP2_VRAM_B0 )
#define RBG0RB_COL_ADR (VDP2_COLRAM + 0x00200)
#define RBG0RA_CEL_ADR (RBG0RB_CEL_ADR + 0x06e80)
#define RBG0RA_MAP_ADR (RBG0RB_MAP_ADR + 0x02000)
#define RBG0RA_COL_ADR (RBG0RB_COL_ADR + 0x00200)
#define RBG0_KTB_ADR (VDP2_VRAM_A1 )
#define RBG0_PRA_ADR (VDP2_VRAM_A1 + 0x1fe00)
#define RBG0_PRB_ADR (RBG0_PRA_ADR + 0x00080)
#define BACK_COL_ADR (VDP2_VRAM_A1 + 0x1fffe)

void ss_main(void)
{
	FIXED posy = toFIXED(0.0);
	ANGLE angz = DEGtoANG(0.0);
	ANGLE angz_up = DEGtoANG(0.0);

	slInitSystem(TV_320x224,NULL,1);
	slTVOff();
	slPrint("Sample program 8.9.2" , slLocate(9,2));

	slColRAMMode(CRM16_1024);

	slRparaInitSet((void *)RBG0_PRA_ADR);
	slMakeKtable((void *)RBG0_KTB_ADR);
	slCharRbg0(COL_TYPE_256 , CHAR_SIZE_1x1);
	slPageRbg0((void *)RBG0RB_CEL_ADR , 0 , PNB_1WORD|CN_12BIT);
	slPlaneRA(PL_SIZE_1x1);
	sl1MapRA((void *)RBG0RA_MAP_ADR);
	slOverRA(0);
	slKtableRA((void *)RBG0_KTB_ADR , K_FIX | K_DOT | K_2WORD | K_ON);
	Cel2VRAM(tuti_cel , (void *)RBG0RA_CEL_ADR , 65536);
	Map2VRAM(tuti_map, (void *)RBG0RA_MAP_ADR, 64, 64, 2, 884);
	Pal2CRAM(tuti_pal , (void *)RBG0RA_COL_ADR , 160);

	slPlaneRB(PL_SIZE_1x1);
	sl1MapRB((void *)RBG0RB_MAP_ADR);
	slOverRB(0);
	slKtableRB((void *)RBG0_KTB_ADR , K_FIX | K_DOT | K_2WORD | K_ON);
	Cel2VRAM(sora_cel , (void *)RBG0RB_CEL_ADR , 28288);
	Map2VRAM(sora_map, (void *)RBG0RB_MAP_ADR, 64, 20, 1, 0);
	Pal2CRAM(sora_pal , (void *)RBG0RB_COL_ADR , 256);

	slRparaMode(K_CHANGE);

	slBack1ColSet((void *)BACK_COL_ADR , 0);

	slScrAutoDisp(NBG0ON | RBG0ON);
	slTVOn();

	while(1)
	{
		slCurRpara(RA);
		slUnitMatrix(CURRENT);
		slTranslate(toFIXED(0.0) , toFIXED(0.0) + posy , toFIXED(100.0));
		posy -= toFIXED(5.0);
		slRotX(DEGtoANG(-90.0));
		slRotZ(angz);
		slScrMatSet();

		slCurRpara(RB);
		slUnitMatrix(CURRENT);
		slTranslate(toFIXED(160.0) , toFIXED(155.0) , toFIXED(100.0));
		slRotZ(angz);
		slScrMatSet();

		angz_up += DEGtoANG(0.5);
		angz = (slSin(angz_up)>> Four);

		slSynch();
	} 
}

Flow 8-8 sample_8_9_2: 3D rotation

▲ Back ｜ Forward ▼
★ SGL User's Manual ★ PROGRAMMER'S TUTORIAL
Copyright SEGA ENTERPRISES, LTD., 1997